This guest post was written by Greg McMillan, industry consultant, author of numerous process control books, 2010 ISA Life Achievement Award recipient and retired Senior Fellow from Solutia Inc. (now Eastman Chemical).
Many important process control loops on vessels and columns do not have a steady state in the time frame of the PID response and are classified as near-integrating as discussed in Part 1 of this blog focus on controller tuning. Integrating and runaway processes have no steady state at all in the operating range of the process. If there is insufficient process control action, these processes can ramp and even accelerate to the violation of an equipment limit or a trip of a safety instrumented system (SIS).
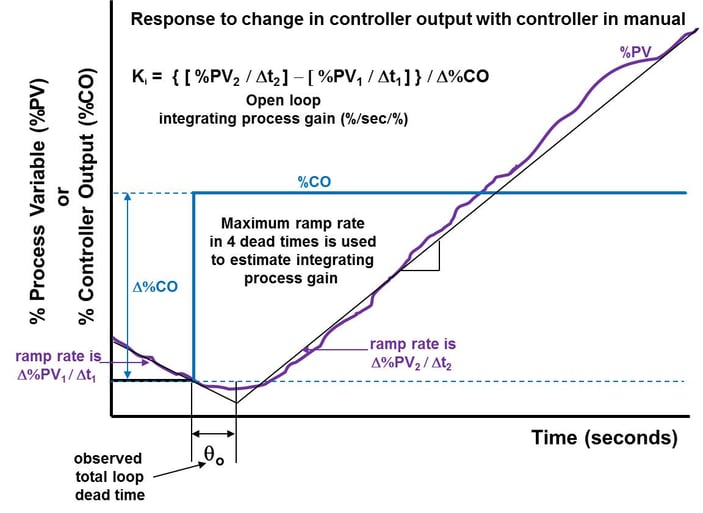
Integrating processes are defined by a total loop dead time and an integrating process gain (see the figure below). A secondary time constant may be used to describe the initial lag (bend) in the response. The integrating process gain is the ramp rate in % of PID input per second divided by the % change in PID output giving a gain of reciprocal time units (1/sec). Level is the most common loop with an integrating response.
Integrating Process Response
Gas pressure has a near integrating or true integrating response depending on the size of the pressure drop across the manipulated valve relative to the changes in pressure during an open loop test. Batch composition, pH, and temperature loops have essentially an integrating response unless altered by a reaction. An integrating process will exhibit self-regulating closed loop response for a proportional only controller. The distance of the new from the initial operating point decreases as the PID gain increases. Integrating and “near integrating” processes require aggressive proportional action. The steady state gain divided by the open loop time constant of a near integrating process is effectively an open loop integrating process gain. The maximum PID gain is inversely proportional to the process time constant or integrating process gain. Most integrating processes are so slow (integrating gain so small) and the dead time is so relatively small that the maximum PID gain so large that the primary limit to how high you set this gain is user knowledge and noise.
The degree of internal negative feedback within the process determines whether the process will quickly settle, ramp, or diverge when the controller is in manual and the PID output is changed. For integrating and runaway processes there is no internal negative feedback and hence no steady state. When internal process negative feedback is absent or even worse is replaced with positive feedback in runaway processes, the amount of negative feedback from the controller must increase principally by an increase in proportional action (controller gain).
The best controller tuning settings can be determined by identifying key dynamic variables that characterize the process response. See the extensively updated Good Tuning: A Pocket Guide 4th Edition for concise guidance on this topic and everything else you need to know to get the most out of your PID controller.
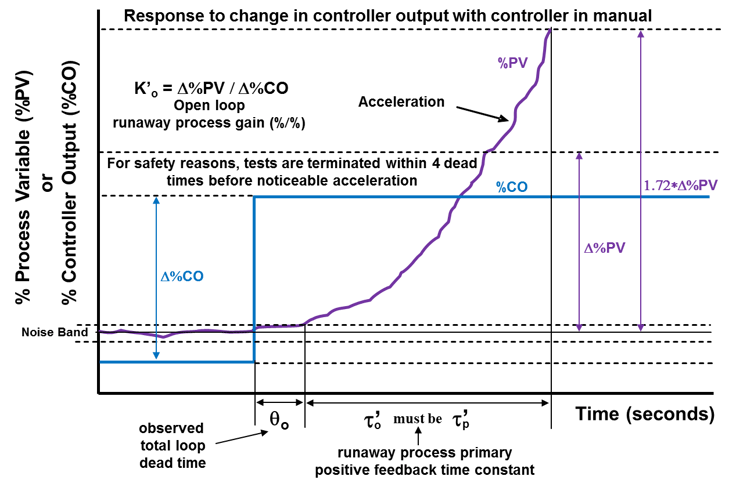
Runaway processes are defined by a total loop dead time, a positive feedback open loop time constant, and an open loop runaway process gain (see the figure). The positive feedback time constant causes the continual acceleration. A secondary time constant may be used to describe the initial lag (bend) in the response. The runaway process gain is best estimated via the ordinary differential equations for the reactor energy balance per Appendix F in the ISA book Advances in Reactor Measurement and Control.
Runaway Process Response
Open loop tests are rarely done in runaway processes because of the safety concerns from the acceleration. Manual control of a runaway process is extremely difficult. Most true runaway processes are always operated in automatic or a higher mode. Tuning tests are done with the PID loops in auto. The large controller gains and integral times used for these loops provide a step change in controller output from the proportional mode and negligible ramping from the integral mode in four dead times. Polymerization and specialty chemical reactors with a heat release from an exothermic reaction that can exceed the cooling rate can develop a runaway response for an increase in temperature.
Determine the type of process response and choose the tuning rules accordingly. Make step changes to the process to identify the total dead time, open loop gain, and secondary time constant. If the process continues to ramp or accelerate in this time frame, the process response is near-integrating, integrating, or runaway. The open loop gain for these processes is an integrating process gain (change in ramp rate divided by change in controller output) and integrating process tuning rules are used. The PID structure and tuning settings must provide immediate action overdriving the PID output past its final resting value by more proportional than integral action. For surge tank level control discussed in a future post, we will see that the controller gain is moderated to maximize the absorption of variability. However, the PID output must still be driven past its final resting value (balance point where manipulated flow equals net load).
About the Author
Gregory K. McMillan, CAP, is a retired Senior Fellow from Solutia/Monsanto where he worked in engineering technology on process control improvement. Greg was also an affiliate professor for Washington University in Saint Louis. Greg is an ISA Fellow and received the ISA Kermit Fischer Environmental Award for pH control in 1991, the Control magazine Engineer of the Year award for the process industry in 1994, was inducted into the Control magazine Process Automation Hall of Fame in 2001, was honored by InTech magazine in 2003 as one of the most influential innovators in automation, and received the ISA Life Achievement Award in 2010. Greg is the author of numerous books on process control, including Advances in Reactor Measurement and Control and Essentials of Modern Measurements and Final Elements in the Process Industry. Greg has been the monthly "Control Talk" columnist for Control magazine since 2002. Presently, Greg is a part time modeling and control consultant in Technology for Process Simulation for Emerson Automation Solutions specializing in the use of the virtual plant for exploring new opportunities. He spends most of his time writing, teaching and leading the ISA Mentor Program he founded in 2011.
Connect with Greg:
