This post was authored by Hans D. Baumann, Ph.D., PE, author of Fluid Mechanics of Control Valves: How Valves Control Your Process and a world-renowned expert on control valve technology. To read a brief author Q&A plus download a free, 42-page excerpt from the book, click this link.
Cavitation is the implosion of tiny vapor bubbles in a liquid when the static pressure reaches the vapor pressure of the specific liquid. This happens when, due to a high pressure differential across a valve, the resultant high velocity lowers the static pressure. Cavitation is a bane for the valve designer and valve user alike. It not only causes severe damage to valve trim, but also creates sound levels that can exceed 110 decibels.
The damage is caused when the imploding vapor bubbles create pressure waves that accelerate at values of 1.5 × 1011 m/s2 and reach velocities of 500 m/s. Even hardened steel cannot resist such an impact, even though the bubble size has a diameter of only about 200 micrometers.
There have been methods to eliminate, or at least reduce, cavitation in throttling valves. The simplest way is to reduce the pressure drop by changing the altitude of a valve or installing two valves in series. However, these approaches are usually not doable because of system restrictions. If possible, one should limit the valve’s pressure drop below the pressure level indicated by the cavitation index Xfz, where Xfz is the allowable delta P divided by inlet pressure minus vapor pressure (pressures in absolute terms). Xfz values may be gleaned from figure 7.
Cv is an industrywide flow coefficient defined as Cv = 1.17 × [ Q / (P1 – P2)0.5], where Q = m3/hr of cold water and P is in bar(abs) = (1 × 105 Pascal). For example, a DN 100 conventional globe valve with a required Cv of 50 has an Xfz factor of 0.34.
Other known ways of fighting cavitation is injecting air into the fluid or using the vacuum pressure created by the cavitating fluid. Figure 1 shows how this can be done. A butterfly valve has a hollow stem conducting outside air into a number of small holes and dispersing the air into the water. This can only be done if the vapor pressure is in a vacuum and if the particular fluid tolerates air inclusion.
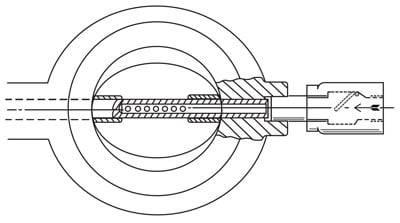Figure 1. A butterfly valve reduces cavitation by utilizing air sucked in by the liquid vapor through a series of holes. A check valve prevents the escape of liquid in case there is no vacuum downstream of the vane.
Another quite effective way of reducing cavitation is by utilizing drilled cages inside globe valves, sometimes using several hundred drilled holes. The effect is twofold. First, the small holes increase the Xfz factor, and second, the resulting small jets create only localized cavitation. The drawback is that this is an expensive solution and cannot readily be scaled up.
Quite often, butterfly valves are used especially in larger sizes due to lower cost. To reduce the tendency to cavitate in such valves, companies employ proprietary vane designs. Figure 2 shows such a design, using a row of teeth on both leading edges of the vane to split up the liquid jets.
Anecdotal information indicates that this design indeed reduces cavitation, as these valves were used successfully in Japan, in sizes up to 2 meters for drinking water pipelines. These valves had the drawbacks that they cannot provide tight shutoff and cannot offer the more popular equal percentage flow characteristic.
Another design solves such deficiencies (figure 3). Here, a low-noise insert is attached to a conventional triple eccentric butterfly valve, which provides shutoff. The attachment not only reduces cavitation (as explained later), but also creates an equal percentage flow characteristic due to the special configuration of the teeth part of the attachment.
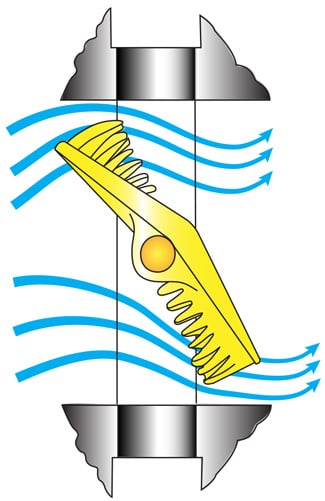Figure 2. A low noise and activation butterfly valve using opposed rows of teeth splitting up the fluid stream, changing frequency, and increasing the Xfz factor. Source: Tomoe Company
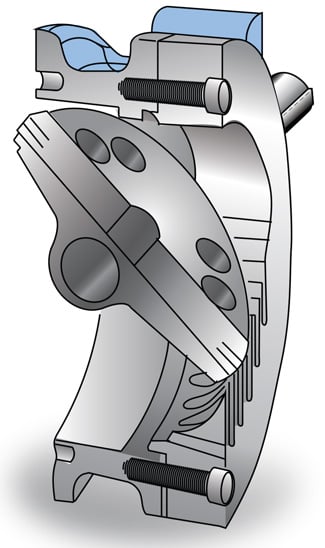Figure 3. A Sharktooth butterfly system using conventional shutoff butterfly valves. By attaching a multitooth element, it has higher fluid resistant and Xfz factors. The teeth profiles provide an equal percentage flow characteristic. Source: Yeary Associates, Inc.
Reducing cavitation
First a little theory: Most of us are by now familiar with the fluid resistant (FL) factor, denoting pressure recovery in a valve. This factor has been an invaluable aid in proper valve sizing, even though the concept of pressure recovery in valves has only been known since 1963.
What most people may not know is that the FL factor tells us how much of the kinetic energy (velocity head) in a valve is converted into turbulence and heat. There is a correlation between FL and the head loss coefficient K or Σ; here K = FL2. Incidentally, FL works for all Newtonian fluids, whether liquids or gases.
Assume a valve has an FL of 1. Here all kinetic energy is converted into heat (turbulence), and therefore, the valve cannot experience cavitation. On the other hand, consider a conventional butterfly valve with a typical FL of 0.65. Here the K factor is 0.422, meaning only 42 percent of the kinetic energy is converted, and the rest is used to evaporate some of the liquid; the vapors then implode in the pressure recovery zone of the valve to cause damage and noise.
Figure 4 shows a pressure diagram using 10 bar absolute as inlet pressure and 4.5 bar as outlet pressure. Using the typical butterfly valve FL of 0.65, we notice a velocity head of 13 bar. This is a theoretical number, since the velocity head cannot exceed the vapor pressure. But what it means is that an energy equivalent of 2 bar is used to evaporate the liquid, and cavitation will occur. On the other hand, if another valve with an FL of 0.84 were used, the velocity head will only be 7.8 bar, and the bottom will stay well above the vapor pressure, hence, no cavitation.
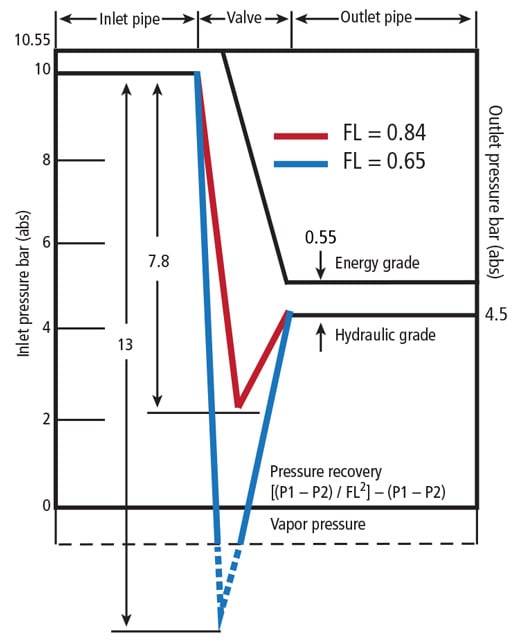Figure 4. Graphic presentation of pressure gradients inside a valve at 5.5 bar pressure drop
Having realized the importance of head loss, it was found that the configuration of the Yeary valve indeed produced sufficient hydraulic friction to yield high FL numbers. The graph in figure 5 shows the results of a water test on a DN 150 (6-inch) valve at 60 degrees open (a large opening for a valve having high pressure drops) and an FL factor of 0.8. Here the inlet pressure was 7.7 bar absolute with pressure drops down to just below 1 bar absolute.
It is perhaps astonishing how closely the calculated levels correspond with the microphone readings. Note that the blue line corresponds to the 30 log(10X) relationship predicted for turbulent water. Cavitation occurs at 5 bar pressure drop (64 percent of the inlet pressure). The cavitation amplitude was calculated as 5.6 dB, which matches the test data. Note that the increase in slope terminates when X is equal to FL2, which happens around a P2 of 3 bar absolute.
To purchase a copy of Fluid Mechanics of Control Valves: How Valves Control Your Process, click this link. To read a brief author Q&A plus download a free, 42-page excerpt from the book, click this link.
This test shows that calculated turbulent water slopes can easily be used to predict the onset of cavitation. In this case it happened around an outlet pressure of 3 bar, as is predicted by the equation: P2cav. = P1 – [(P1 – Pv) × FL2], which calculates the limit to be 2.8 bar. The estimated cavitation sound level closely matches the test data despite a lack of test points. As shown in the graph, when the outlet pressure dips into vacuum, water saturates with vapor, and there is a sudden drop in sound.
These tests have been duplicated at 20 and 30 degrees opening, yielding almost identical results. At 20 degrees open, for example, the 0.150 valve only started cavitating at an Xfz of 0.83 with a cavitation amplitude of only 3 dB.
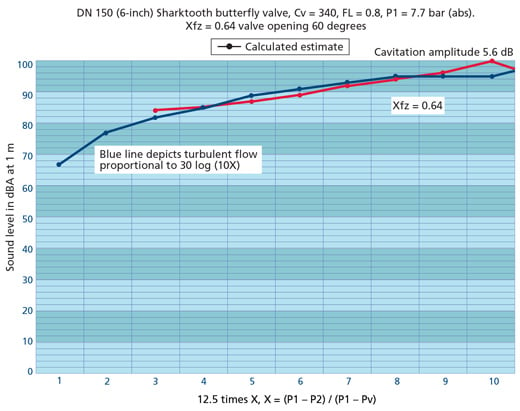Figure 5. Results of a water test on a DN 150 (6”) valve at 60 degrees open and an FL factor of 0.8
As shown in figure 6 (below), the cavitation only happens at a high pressure drop of 6.3 bar (X = 0.81). The cavitation amplitude of 3 dB matches the prediction, where amplitude = 60 log (Xy / Xfz), Xfz = 0.81, and Xy = 0.91. The apparent discrepancy of 4 dB and 5 dB between test data and calculations can partially be explained by significant pump noise in the laboratory.
All tests confirm the exceptional high conversion rate of dynamic fluidic energy to static energy, thus avoiding cavitation in all but the very high pressure drop regions. As the designer of the valve, I can attest to the veracity of these features. These tests also show that sound can play an important role in testing valves for cavitation characteristics.
A globe valve is a two-stage device consisting of a plug and seat ring having an FL of perhaps 0.6, implying an Xfz factor of 0.36. The valve body, having a tortuous flow path, may have an FL of 0.9, making the overall FL = 0.82. Here the governing Xfz is that of the valve trim (where cavitation actually occurs), and the relationship Xfz = square root of overall FL does not apply.
All tests were performed at the Utah State Water Research Laboratory in Logan, Utah, under the guidance of Professor Michael Johnson, PhD, PE. I thank Dr. Johnson for his help and valuable advice.
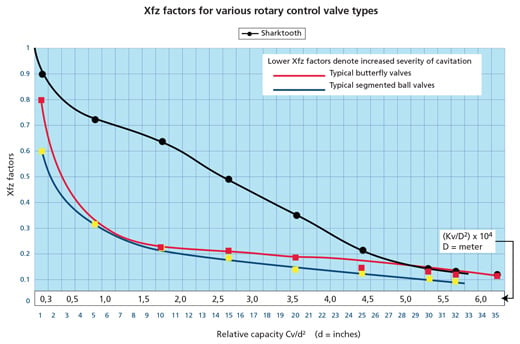Figure 7. Xfz values. Note that the graph shows both the European (in meters) and the U.S. (in inches) systems on the x-axis.
Graph references: IEC 60534-8-4: Prediction of noise generated by hydrodynamic flow and “A fresh look: How to estimate cavitation noise” Valve World, by H.D. Baumann
A version of this article also was published at InTech magazine.
