This post is an excerpt from the journal ISA Transactions. All ISA Transactions articles are free to ISA members, or can be purchased from Elsevier Press.
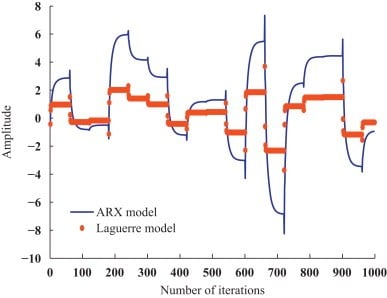
Abstract: In this paper, we propose a new reduced complexity model by expanding a discrete-time ARX model on Laguerre orthonormal bases. To ensure an efficient complexity reduction, the coefficients associated to the input and the output of the ARX model are expanded on independent Laguerre bases, to develop a new black-box linear ARX-Laguerre model with filters on model
Validation of the Laguerre model.
input and output. The parametric complexity reduction with respect to the classical ARX model is proved theoretically. The structure and parameter identification of the ARX-Laguerre model is achieved by a new proposed approach which consists in solving an optimization problem built from the ARX model without using system input/output observations. The performances of the resulting ARX-Laguerre model and the proposed identification approach are illustrated by numerical simulations and validated on benchmark manufactured by Feedback known as Process Trainer PT326. A possible extension of the proposed model to a multivariable process is formulated.
Free Bonus: To read the full article on decomposition of an ARX model, click here.
ISA membership entitles you to free access to all ISA Transactions articles plus a wealth of technical content, industry information, free webinars, training opportunities, program discounts, certification and licensure and professional networking.
Join ISA ... learn, advance, succeed!
2006 Elsevier Science Ltd. All rights reserved.
