This post was written by Greg McMillan, industry consultant, author of numerous process control books, 2010 ISA Life Achievement Award recipient and retired Senior Fellow from Solutia Inc. (now Eastman Chemical).

The proportional, integral, derivative (PID) controller is the common key component of all control loops. Basic control systems depend upon the PID to translate the measurement signals into set points of secondary loop controllers, digital valve controllers, and speed controllers for variable frequency drives. The success of advanced control, such as model predictive control, depends upon the basic control system foundation and hence the PID.  

Elmer Sperry developed the first example of the PID in 1911, and Nicolas Minorsky published the first theoretical analysis in 1922. Ziegler and Nichols published papers on the ultimate oscillation method and reaction curve method for controller tuning in 1942 and 1943. While the parameters chosen as factors in the tuning settings provided overly aggressive control, the basic premise of an ultimate gain and ultimate period is essential to the fundamental understanding of the limits of stability.

The identification of the slope in the reaction curve method is a key to the use of the near-integrator concept that we will find here to be critical for most composition, temperature, and pH loops to improve tuning settings and dramatically shorten test times. Bohl and McAvoy published a paper in that showed the PID can provide nearly optimal control for unmeasured load disturbances. Shinskey wrote many books detailing the knowledge of process dynamics and relationships essential to the best application of PID control.

Shinskey developed the original equation for integrated error from disturbances as a function of tuning settings, as detailed in the article PID tuning rules. Shinskey also published a book dedicated to PID controllers that showed the simple addition of a dead time block in the external reset feedback path could further enhance the PID performance by dead time compensation. Internal model control (IMC) and lambda tuning rules were developed based on pole and zero cancellation to provide a good response to set points and disturbances at the process outlet. However, most of the improvement in set point response could have been achieved by a set point lead-lag or PID structure. Also, these tuning rules do not perform well for the more common case of disturbances on the process input (load upsets), particularly for lag dominant processes.

Skogestadt developed significant improvements to IMC tuning rules. Bialkowski showed that always using lambda rather than lambda factors, relating lambda to dead time, and treating lag dominant processes as near-integrators enable the PID to provide good nonoscillatory control for load upsets besides dealing with the many different difficulties and objectives for which lambda tuning was originally designed. Not realized is that most methods converge to the same basic expression for the PID gain and reset time when the objective is load disturbance rejection and that a tuning parameter that is the closed loop time constant or arrest time is set relative to dead time.

Also not recognized is how PID features, such as structure, external reset feedback, enhanced PID for analyzer and wireless, simple calculation of a future value, valve position controller, and “full throttle” set point response, can increase process efficiency and capacity, as noted in the ISA book 101 Tips for a Successful Automation Career.  

Overload

The user is confronted with considerable disagreement of tuning rules as seen in the 400 pages of tuning rules in the 2006 book by O’Dwyer, not realizing most of them can be adjusted by factors or a near-integrator concept to achieve good control. The modern PID has many more options, parameters, and structures that greatly increase the power and flexibility of the PID, but most are underutilized due to insufficient guidance. Additionally, ISA standard form used in most modern control systems is not the parallel form shown in most textbooks or the PID series form pervasively used in the process industry until the 1990s.

All of this can be quite overwhelming to the user, particularly because tuning is often done by a generalist faced with rapid changes in technology and with many other responsibilities. My goal in my recent articles, books, and columns (including blogs), which are more extensive and less supplier-specific than white papers, is to provide a unified approach and more directed guidance based on the latest PID features that are missing in the literature.

Good Tuning: A Pocket Guide, Fourth Edition seeks to concisely present the knowledge needed and to simplify the tuning by switching between just two sets of tuning rules, largely depending upon whether the PID is a primary or secondary controller. A primary PID for vessel or column composition, gas pressure, level, pH, and temperature control uses integrating process tuning rules where the lambda arrest time is set. A secondary PID for liquid pressure, flow, inline pH, and heat exchanger temperature control, uses self-regulating process tuning rules where the closed loop time constant is set. In both situations, lambda rather than a lambda factor is used and chosen relative to the dead time to provide the degree of tightness of control and robustness needed. The best thing a user can do is to use good tuning software, attend supplier schools, and get a consultant in the plant for on-site solutions and practice. It is also important to take responsibility for avoiding common tuning mistakes. Here we step back to make sure we are not susceptible to oversights and misunderstandings. The following compilation has the most common, disruptive, and potentially unsafe mistakes first, but all can come into play and be important.  

Mistakes

1. Using the wrong control action: In analog controllers and in many early distributed control systems (DCSs) and programmable logic controllers (PLCs), the valve action affected only the display of the output on the station or faceplate. The specification of an “increase-to-close” valve action for a fail-open valve reversed the display but not the actual output. Consequently, the control action had to take into account the valve action besides the process action. If the valve was “increase-to-open” (fail close), the control action was simply the reverse of the process action (direct control action for reverse-acting process and vice versa). If the valve was “increase-to-close” the control action was the same as the process action (direct control action for direct-acting process and vice versa) if not reversed in the current-to-pneumatic (I/P) transducer or positioner. In today’s systems, the user can specify “increase-to-close” in the PID block or analog output block besides the digital valve controller, enabling the control action to be set as the opposite of the process action. The challenge is realizing this and making sure the increase-to-close valve action is only set in one place. If you do not get the control action right, nothing else matters (the PID will walk off to its output limit).

2. Using PID block default settings: The settings that come with a PID block as it is dragged and dropped into a configuration must not be used. When first applying PID to dynamic simulations of new plants, typical settings based on process type and scale span can be used as a starting point. However, tuning tests must be done and settings adjusted before operator training and loop commissioning.

3. Using parallel form and series tuning settings in the ISA standard form: A parallel form that uses integrator gain and derivative gain settings that are put into the ISA standard form as reset time and rate time settings can be off by orders of magnitude. A series form can provide good control with the rate time equal to or greater than the reset time. This is because interaction factors inherently reduce the PID gain and rate time and increase the PID reset time to prevent oscillations from the derivative mode contribution being greater than the contribution from the other modes. Using a rate time equal to or greater than the reset time in an ISA standard form can cause severe fast oscillations.

4. Using the wrong units for tuning settings: Here we consider just the series form and ISA standard form. Controllers can have a gain or proportional band setting for the proportional mode. The gain setting is dimensionless and is 100 percent divided by the proportional band. Some PID algorithms in control studies and actual industrial systems have the gain setting in engineering units, which leads to a very bizarre setting. The integral mode setting can be repeats per second, repeats per minute, minutes per repeat, or seconds per repeat. The units of these last two settings are commonly given as just minutes or seconds. The omission of the “per minute” can cause confusion in the conversion of settings. The conversion of the rate time is simpler, because the units are simply minutes or seconds.

5. Using the wrong units for output limits and anti-reset limits: In analog controllers and in many early DCS and PLC systems, the output and consequently the output limits and anti-reset windup limits were in percent. In modern control systems, the output is in engineering units, and the limits must be set in engineering units. For valves, the units are usually percent of valve stroke. For a primary (upper) PID that is sending a set point to a secondary (lower) PID, the primary PID output is in the engineering units of the secondary PID process variable.

6. Tuning level controllers: If you calculate the product of the valve, gain, process gain, and measurement gain, where the process gain is simply the inverse of the product of the fluid density and vessel cross-sectional area, you realize the open loop integrating process gain is very small (e.g., 0.000001 1/sec), leading to a maximum PID gain for stability that is more than 100. For surge tank level control, a PID gain closer to unity is desired to absorb fluctuations in inlet flows without passing them on as changes to a manipulated outlet flow that will upset downstream users. Users do not like a high PID gain even when tight level control is needed. Decreasing the level controller gain without a proportional increase in the reset time will cause nearly sustained slow rolling oscillations. Further decreases in the PID gain only make the oscillations worse. Most oscillations in production plants and poor performance of distillation columns can be traced back to poorly tuned level controllers. The solution is to choose an arrest time (lambda for integrating processes) to either maximize the absorption of variability (e.g., surge tanks level control or distillate receiver level control where distillate flow is manipulated) or maximize the transfer of variability (e.g., reactor level for residence time control or distillate receiver level control where reflux flow is manipulated for internal reflux control). The integrating process tuning rules prevent the violation of the window of allowable PID gains by first setting the arrest time and using this time to compute the reset time and finally the PID gain.

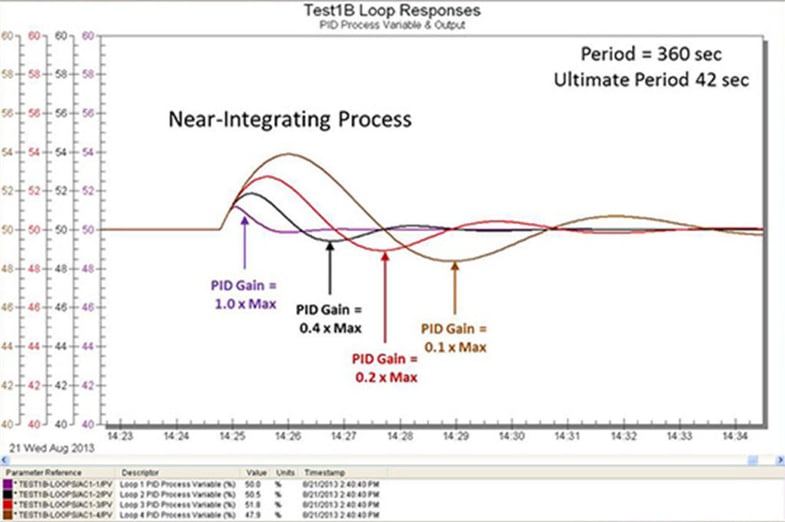
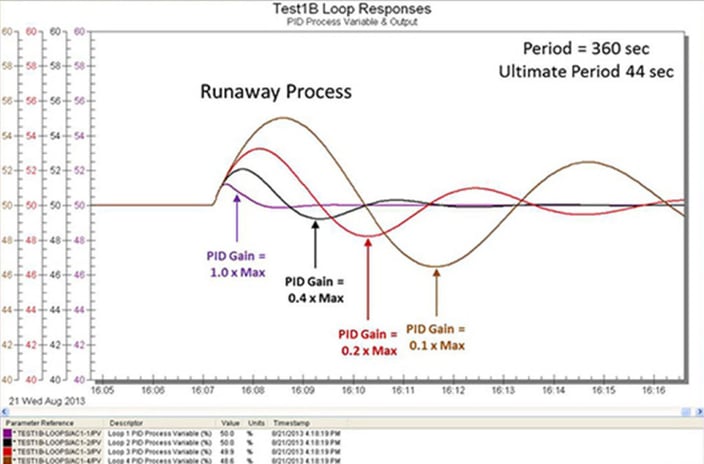
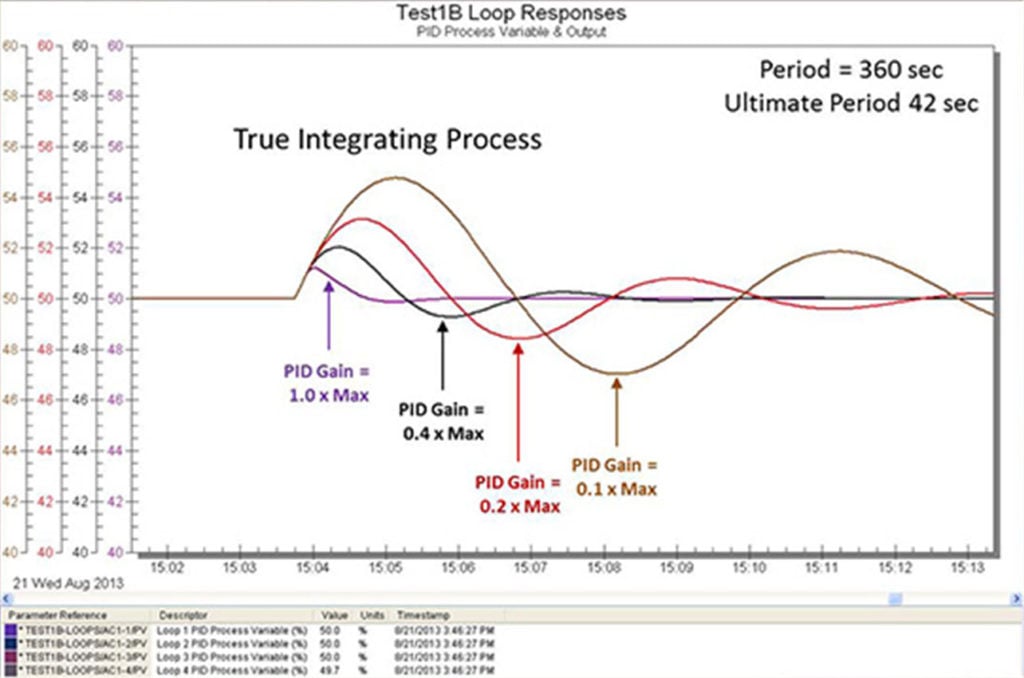
7. Violating the window of allowable controller gains: We can all relate to the fact that too high of a PID gain causes oscillations. In practice, what we see more often is oscillations from too low of a PID gain in primary loops. Most concentration and temperature control systems on well-mixed vessels are vulnerable to a PID gain that violates the low PID limit, causing slow rolling, nearly undamped oscillations. These systems have a highly lag dominant (near-integrating), integrating, or runaway process response. All of these processes benefit from the use of integrating process tuning rules to prevent the PID gain from being less than twice the inverse of the product of the open loop integrating process gain and reset time, preventing the oscillations shown in the figures. The oscillations in the figures could have been stopped by increasing the reset time. In industrial applications, the reset time in vessel control loops often needs to be increased by two or more orders of magnitude. Note that the oscillations get worse as the process loses internal self-regulation, going from a near-integrating (low internal negative feedback) to an integrating (no internal feedback) and to a runaway (positive feedback) open loop response. For runaway processes, there is also a minimum gain setting independent of reset time that is the inverse of the open loop runaway process gain. The identification of the open loop integrating process gain can generally be done in about four dead times, greatly reducing the test time and reducing the vulnerability to load upsets.

8. Lacking recognition of sensor lag, transmitter damping, or filter-setting effect: A slow measurement response can give the illusion of better control. If the measurement time constant becomes the largest time constant in the loop, the PID gain can be increased and oscillations will be smoother as the measurement is made slower. This occurs all the time in flow control, pressure control, inline pH control, and temperature control of gas volumes, since the process time constant is less than a second. The real process variability has increased and can be estimated with a simple equation. For more information about this widespread problem, see the Control Talk blog Measurement Attenuation and Deception Tips. For details about how to prevent this in temperature control systems, see the ISA Interchange post Temperature Sensor Installation for Best Response and Accuracy.

9. Failing to do tuning tests at different times, set points, and production rates: The installed characteristics of most control valves and most concentration, pH, and temperature processes are nonlinear. The process gain varies with operating point and process conditions, including relatively unknown changes in catalyst activity, fouling, and feed compositions. The valve gain varies with system resistances and flow required. For operating point nonlinearities, the open loop process gain identified depends upon the step size and direction and the split range valve being throttled. Temperature process time constants also tend to vary with the direction of the change. For more details see the Control Talk blog post Why Tuning Tests are Not Repeatable.

10. Failing to increase PID gain to decrease backlash limit cycle amplitude: An attempt to decrease oscillation amplitude by decreasing gain will make the oscillation worse when the oscillation is a limit cycle from backlash (deadband). The amplitude from backlash is inversely proportional to the PID gain. The limit cycle period from backlash or stiction is also increased as the PID gain is decreased, reducing the attenuation from the filtering effect of process volumes. The same equation noted in item 8 can be used to estimate the attenuated amplitude at the outlet of a well-mixed volume by using the residence time (volume divided by throughput flow) as the filter time constant. Having avoided mistakes, you are ready to take full advantage of the online addendum below on top PID control opportunities.  

War Stories

1) The trend charts of phosphorous furnace pressure from faster pressure transmitters installed looked worse, even though the number of high-pressure reliefs had been dramatically reduced. Fortunately, the older, slower transmitters were left installed, showing that the amplitude of the pressure excursions had actually decreased after the faster transmitters were used for furnace pressure control. 2) A plant operated for several years with default tuning settings of gain and reset (repeats per minute) both equal to 1 for all of the PID controllers. Nearly every loop was oscillating, but the plant ingeniously managed to run by setting output limits to reduce oscillation amplitudes. 3) When a plant converted from analog controllers to a DCS, the plant was amazed at the improvement in the distillation column control. It turns out the configuration engineers did not realize the difference between PID gain and proportional band (PB). The analog controller for column overhead receiver level manipulating reflux had a PB of 100 percent that was then set as the gain of 100 in the DCS PID. The tight level control and consequential great internal reflux control stopped the slow rolling oscillations from violation of the low gain limit and rejected disturbances from “Blue Northerner” cold rain storms.

Addendum

Top PID control opportunities

1. Use cascade control, so secondary proportional, integral, derivative (PID) controllers (e.g., flow and jacket temperature controllers) isolate the primary PID controllers (e.g., composition, level, pH, and temperature) from the nonlinearities of the control valve installed flow characteristic, pressure disturbances, and process nonlinearities, and to enable feedforward and ratio control. If the flowmeter does not have the rangeability needed, substitute an inferential flow measurement using the installed valve flow characteristic when the flow drops to the point where the meter signal is too noisy or erratic. (See Control Talk blog entries Best Control Valve Installed Flow Characteristic and Secondary Flow Loop and Valve Positioner Tips.) The exception is that pressure controller outputs must usually go directly to the final control elements (e.g., control valve or variable frequency drive) to provide a faster response. Often the installed valve flow characteristic is linear for these pressure loops by the use of linear trim, because the pressure drop is relatively constant. Use external reset feedback (e.g., dynamic reset limit) to ensure the primary PID output does not change faster than the secondary PID process variable can respond.
2. Use feedforward control that nearly always ends up being ratio control, where the divisors and numerators are most often a flow rate but can be a speed or an energy rate. The ratio is corrected by a primary PID controller. The operator should be able to set the desired ratio and see the actual corrected ratio. Dynamic compensation should be applied as needed so that the manipulated flow arrives at the same point and at the same time in the process as the feedforward flow. Often this is done by inserting adjustable dead time and lead/lag blocks in the feedforward signal. To synchronize the timing of reactant flows or blend flows so that the stoichiometric ratio is maintained for changes in production rates and corrections in ratio, a leader set point is filtered and a ratio factor applied to become the set points of the other flow controllers. Each flow PID is tuned for a smooth response that is fast enough to deal with pressure disturbances and valve nonlinearities. The leader set-point filter is set large enough that all the flow loops respond in unison. (See Feedforward control enables flexible, sustainable manufacturing)
3. Use the right PID structure. The PI on error and D on error structure is often the right choice. If the process variable can only respond in one direction, which may be the case for batch processes with no reaction or change phase and no split-ranged opposing valve (e.g., temperature control with heating but no cooling, and pH control with base reagent but no acid reagent), a structure without integral action is needed (P on error and D on PV no I). In these cases the bias is set to be the PID output when the PID process variable has settled out close to the set point. If overshoot of set point is critical and the time to reach set point and load disturbance response is of no concern, a structure of I on error and PD on PV can be used. A more flexible approach uses a two-degrees-of-freedom PID structure, where the set point weight factors beta and gamma are set for the proportional and derivative modes, respectively, to optimize a compromise between the objectives for set point response and load response. Alternatively, a set point lead-lag can be used to achieve the desired set point response with a PID tuned for a good load disturbance response (minimum peak and integrated absolute errors). See Appendix C of Good Tuning: A Pocket Guide for details on what affects these errors. The set point lag is set equal to the PID reset time, and the lead is set to provide a faster set point response. A lead of zero is equivalent to a PID controller with no proportional or derivative action on error (e.g., beta and gamma equal to zero).
4. Tune all the loops in the right order using good software. Choose tuning rules (e.g., self-regulating versus integrating process) recognizing that self-regulating processes with time constant to dead time ratios greater than 4 can be considered to have a near-integrating response and should use integrating process tuning rules. Use tuning factors (e.g., lambda relative to dead time) based on different objectives (e.g., set point versus load response and maximizing transfer of variability versus maximizing absorption of variability) and difficult situations (e.g., resonance, interaction, and inverse response). See table D-1 in Appendix D of Good Tuning: A Pocket Guide for details. The direction should in general proceed from upstream to downstream PID. The gas and liquid pressure PID controllers should be tuned first, followed by the secondary PID flow and utility system controllers. The level PID controllers should then be tuned for the right objective that depends upon whether the level PID is responsible for enforcing a material balance (e.g., column temperature controller manipulating reflux flow) or just needs to keep the level in bounds because the manipulated flow upsets downstream unit operations (e.g., column temperature controller manipulating distillate flow). Finally, the primary concentration, pH, and temperature controllers should be tuned for the desired set point or load response and the abruptness of movement of the manipulated flow allowed when they can upset other users or come back to upset the respective loop (e.g., plug flow systems with heat integration and recycle streams). If the primary PID does not have a near-integrating, true integrating, or runaway response, and peak error and rise time is not a concern, an objective of minimizing overshoot of the primary PID output past the final resting value may be advantageous. Secondary PID or analog output set point rate limits with primary PID external reset feedback can prevent abrupt changes.
5. Use adaptive control. The PID controller tuning settings generally change with the split-ranged manipulated variable with production rate, heat transfer surface fouling, catalyst activity, and set point, and with cycle time for batch processes (e.g., batch level, reaction rate, and concentration).

Also, see the article Overcoming challenges of PID controller and analyzer applications for the opportunities of using an enhanced PID.

About the Author
Gregory K. McMillan, CAP, is a retired Senior Fellow from Solutia/Monsanto where he worked in engineering technology on process control improvement. Greg was also an affiliate professor for Washington University in Saint Louis. Greg is an ISA Fellow and received the ISA Kermit Fischer Environmental Award for pH control in 1991, the Control magazine Engineer of the Year award for the process industry in 1994, was inducted into the Control magazine Process Automation Hall of Fame in 2001, was honored by InTech magazine in 2003 as one of the most influential innovators in automation, and received the ISA Life Achievement Award in 2010. Greg is the author of numerous books on process control, including Advances in Reactor Measurement and Control and Essentials of Modern Measurements and Final Elements in the Process Industry. Greg has been the monthly "Control Talk" columnist for Control magazine since 2002. Presently, Greg is a part time modeling and control consultant in Technology for Process Simulation for Emerson Automation Solutions specializing in the use of the virtual plant for exploring new opportunities. He spends most of his time writing, teaching and leading the ISA Mentor Program he founded in 2011.

Connect with Greg:

A version of this article also was published at InTech magazine.