AutoQuiz is edited by Joel Don, ISA's social media community manager.
This automation industry quiz question comes from the ISA Certified Control Systems Technician (CCST) program. Certified Control System Technicians calibrate, document, troubleshoot, and repair/replace instrumentation for systems that measure and control level, temperature, pressure, flow, and other process variables. Click this link for more information about the CCST program.
Differential pressure transmitters measure level by inference from:
a) capacitance
b) conductivity
c) hydrostatic head
d) thermal energy
e) none of the above
One can measure (infer) a liquid level by measuring a differential pressure (d/p) caused by the weight of the fluid column in a vessel balanced against a reference. For vessels at atmospheric pressure, the high side of the instrument connects to the bottom of the vessel, and the low side (reference) vents to the atmosphere. This method of level measurement is hydrostatic tank gauging.
The reference can also be a column of fluid of fixed height such as a liquid-filled reference leg outside the tank or, as in the case of a bubbler system, a gas-filled reference leg usually inside the tank.
The key requirement is that the reference leg provide (or represent) a constant, known, hydrostatic head. To obtain an accurate measurement using d/p cells, one must know the densities of the process liquid and of the reference leg liquid.
Mathematically, the d/p relationship yields level by solving this equation for h:
P = P0 + ρ (g/gc) h . . . where g/gc is the conversion factor 9.8066 N/kg.
Graphically, the d/p and level relationship looks like this.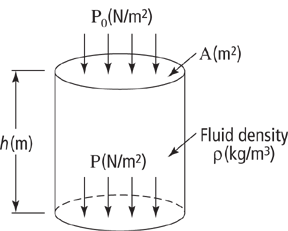
The correct answer is C .
About the Editor
Joel Don is the community manager for ISA and is an independent content marketing, social media and public relations consultant. Prior to his work in marketing and PR, Joel served as an editor for regional newspapers and national magazines throughout the U.S. He earned a master's degree from the Medill School at Northwestern University with a focus on science, engineering and biomedical marketing communications, and a bachelor of science degree from UC San Diego.




